1. Введение
Гусеничная платформа с дифференциальным приводом предназначена для работы в условиях сложного рельефа и нестабильных поверхностей. Платформа обеспечивает высокую проходимость за счет распределения нагрузки на большую площадь контакта с поверхностью.
Ключевые особенности:
- • Дифференциальная система управления
- • Низкое удельное давление на грунт
- • Возможность поворота на месте
- • Высокая тяговая способность
Области применения:
- • Поисково-спасательные операции
- • Исследование труднодоступных территорий
- • Военные и оборонные задачи
- • Сельскохозяйственные работы
2. Кинематическая модель
Платформа моделируется как твердое тело на плоскости с двумя независимыми гусеницами. Система координат связана с центром масс платформы.
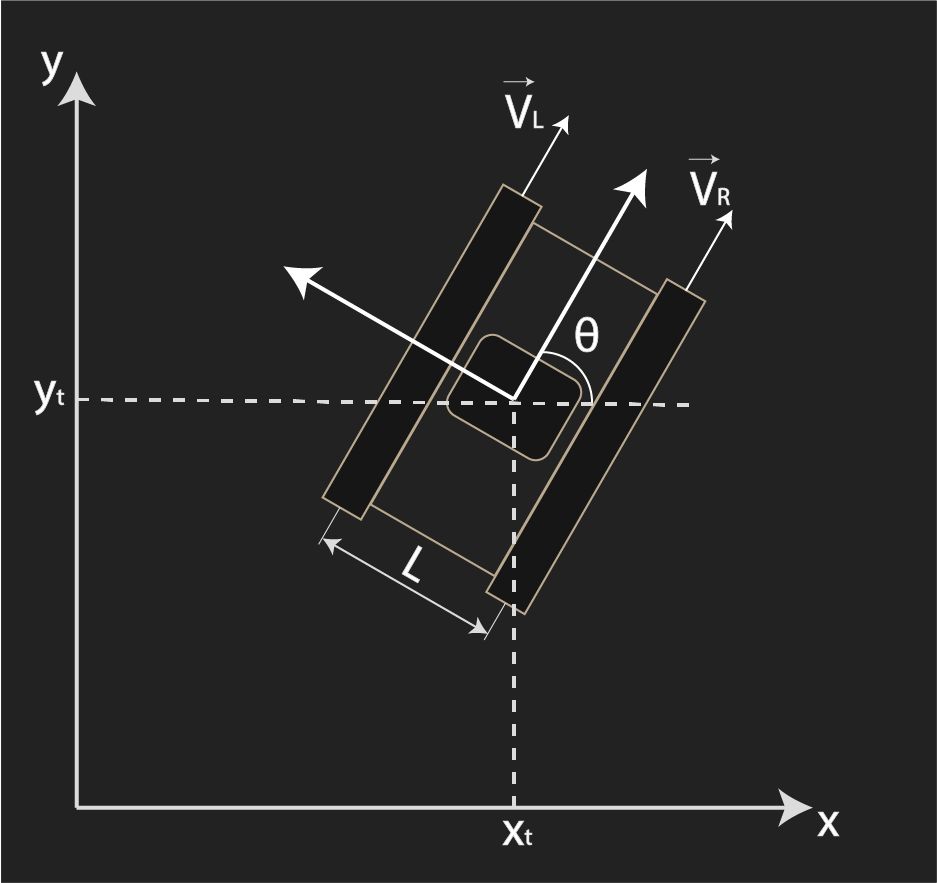
Рис. 1 - Система координат и основные параметры
Параметры системы:
- (x,y) - координаты центра масс в глобальной системе координат
- θ - угол ориентации платформы относительно оси X
- vL, vR - линейные скорости левой и правой гусениц
- L - расстояние между центрами гусениц
Основные уравнения кинематики:
v = (vR + vL) / 2
Линейная скорость центра масс
ω = (vR - vL) / L
Угловая скорость вращения
ẋ = v · cos(θ)
ẏ = v · sin(θ)
θ̇ = ω
Уравнения движения в глобальной системе координат
Режимы движения:
- Прямолинейное движение: vL = vR
- Поворот с радиусом R: vR ≠ vL
- Поворот на месте: vR = -vL
R = (L/2) · (vR + vL) / (vR - vL)
Радиус поворота платформы
3. Динамическая модель
Динамическая модель описывает движение платформы с учетом действующих сил и моментов.
Силы, действующие на платформу:
- FG = m·g - сила тяжести
- NL, NR - нормальные реакции опоры
- TL, TR - силы тяги гусениц
- Fres - сила сопротивления движению
m · dv/dt = (TL + TR) - Fres
Уравнение поступательного движения
J · dω/dt = (TR - TL) · L/2 - Mres
Уравнение вращательного движения
J = (m/12) · (a² + b²)
Момент инерции прямоугольной платформы
Ограничения по сцеплению:
TL ≤ μ · NL
TR ≤ μ · NR
Максимальная сила тяги ограничена сцеплением
Коэффициент проскальзывания:
s = (vtheoretical - vactual) / vtheoretical
Определяет эффективность передачи тяги
Движение на наклонной поверхности:
Fslope = m · g · sin(α)
Составляющая силы тяжести вдоль склона
NL = (m · g · cos(α))/2 - (m · g · sin(α) · h)/L
NR = (m · g · cos(α))/2 + (m · g · sin(α) · h)/L
Распределение нормальных реакций на склоне
αmax = arctan(μ)
Максимальный угол подъема
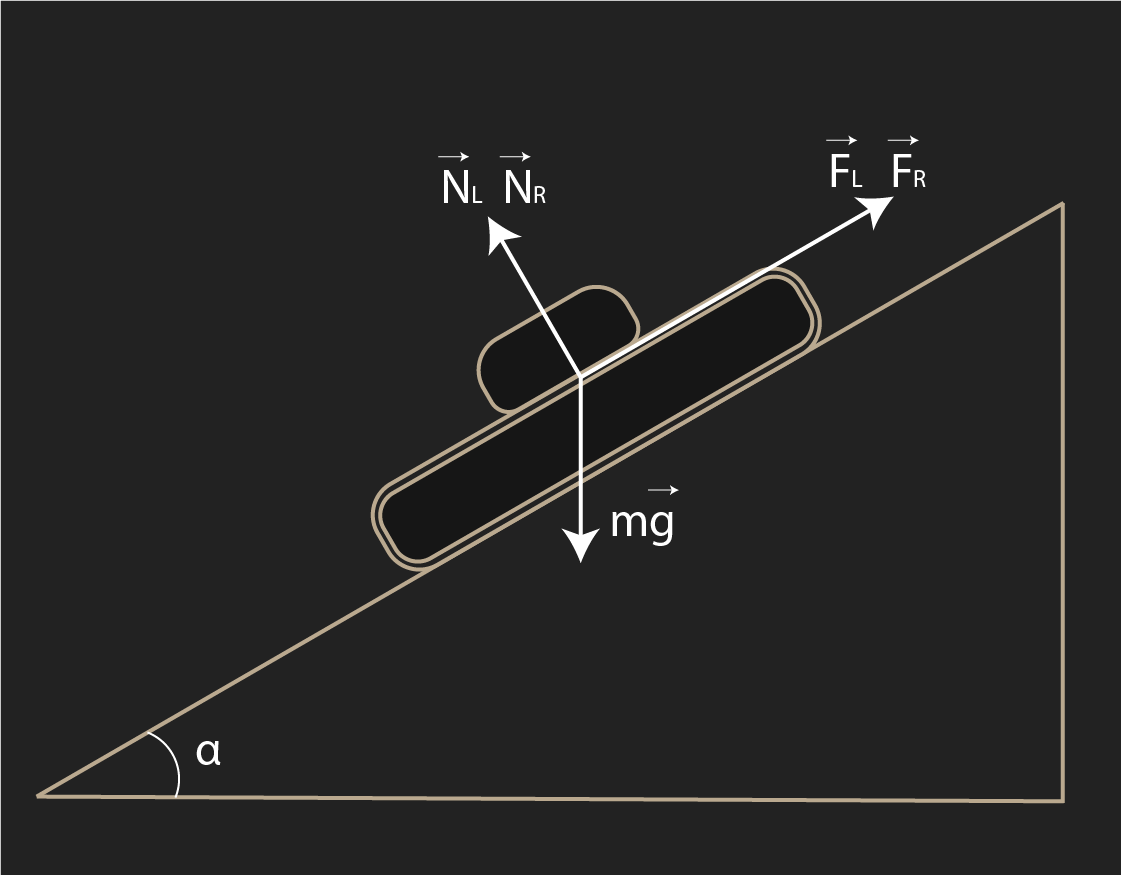
Рис. 2 - Действующие силы
4. Система управления
Система управления построена по иерархическому принципу с тремя уровнями.
Архитектура системы:
- Верхний уровень - планирование траектории
- Средний уровень - управление движением
- Нижний уровень - управление приводами
// Псевдокод управления движением
function controlLoop(x_desired, y_desired, theta_desired) {
// Вычисление ошибки
error_x = x_desired - x_actual;
error_y = y_desired - y_actual;
error_theta = theta_desired - theta_actual;
// ПИД-регуляторы
v_control = pid_v(error_distance);
omega_control = pid_omega(error_theta);
// Преобразование в скорости гусениц
vL = v_control - (omega_control * L) / 2;
vR = v_control + (omega_control * L) / 2;
}
function controlLoop(x_desired, y_desired, theta_desired) {
// Вычисление ошибки
error_x = x_desired - x_actual;
error_y = y_desired - y_actual;
error_theta = theta_desired - theta_actual;
// ПИД-регуляторы
v_control = pid_v(error_distance);
omega_control = pid_omega(error_theta);
// Преобразование в скорости гусениц
vL = v_control - (omega_control * L) / 2;
vR = v_control + (omega_control * L) / 2;
}
Преобразование скоростей:
vL = v - (ω · L)/2
vR = v + (ω · L)/2
Обратное кинематическое преобразование
5. Технические характеристики
| Параметр | Значение | Единицы |
|---|---|---|
| Масса платформы | 1.5 | кг |
| Расстояние между гусеницами (L) | 0.16 | м |
| Максимальная скорость | 2.0 | м/с |
| Максимальная угловая скорость | 1.5 | рад/с |
| Коэффициент сцепления (грунт) | 0.3-0.7 | - |
| Момент инерции (J) | 4.17 | кг·м² |